Trigonometrische Funktionen

Summenformeln

9. Summenformeln

SO NICHT

Motivation:
Von einigen Winkel sind die exakten Werte für sin, cos und tan bekannt:

$$\sin 30^o = \frac{1}{2}, \quad \sin 45^o = \frac{1}{2}\sqrt{2}.$$

Schön wäre es, wenn $\sin (45^o + 30^o) = \sin 45^o + \sin 30^o$ sein würde.

Diese Beziehungen zwischen sin und cos bezeichnet man als Additionstheoreme:

$$\begin{eqnarray*} \sin (\alpha \pm \beta) &=& \sin\alpha\cos\beta \pm \sin\beta\... ...alpha \pm \beta) &=& \cos\alpha\cos\beta \mp \sin\alpha\sin\beta \end{eqnarray*}$$

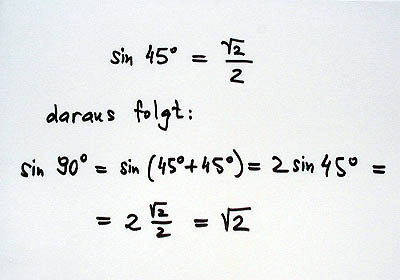
Wer kennt einen geometrischen Beweis?

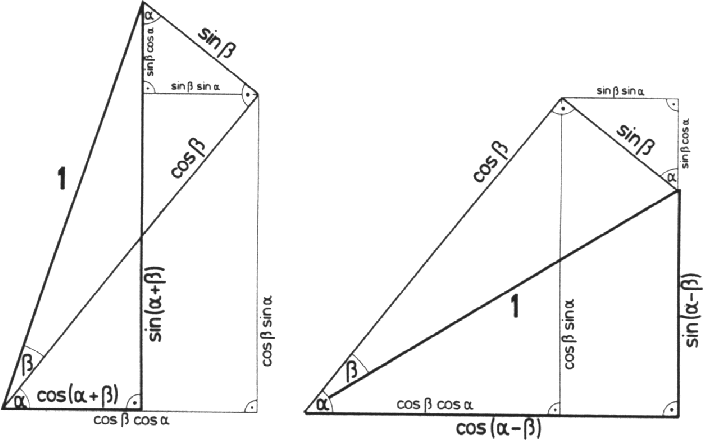
Am interessantesten scheint jedoch das Additionstheorem für den Tangens zu sein - im Hinblick auf die Berechnung des Schnittwinkels zweier Geraden:

$$\tan (\alpha + \beta) = \frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}$$

bzw.

$$\tan (\alpha_2 - \alpha_1 ) = \tan\varphi = \left\vert \frac{m_2 - m_1}{1 + m_2 m_1} \right\vert$$

Aufpassen:

Alle Tangenswerte müssen definiert sein, d. h. $\alpha$, $\beta$, $\alpha+\beta$ $\not=\frac{\pi}{2}+k\pi, \quad k \in Z\hspace{-2.2mm}Z$.
Oft folgen dann noch die Doppelwinkel-Formeln

$$\begin{eqnarray*} \sin 2\alpha & = & 2\sin\alpha\cos\alpha\\ \cos 2\alpha & = &... ...)^2-1\\ \tan 2\alpha & = & \frac{2\tan\alpha}{1-(\tan\alpha)^2} \end{eqnarray*}$$

und die Halbwinkel-Formeln:

$$\begin{eqnarray*} \left(\sin\frac{\alpha}{2} \right)^2 & = & \frac{1}{2}(1-\cos\... ...rac{\alpha}{2} \right)^2 & = & \frac{1-\cos\alpha}{1+\cos\alpha} \end{eqnarray*}$$

Frage:    Was bringen Sie uns?

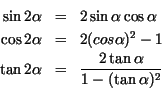
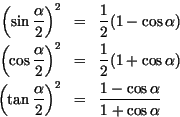
Weiter gibt es noch die Produkt-Summen-Formeln und die Summen-Produkt-Formeln, die hier jedoch nicht weiter angegeben werden sollen ([3], S. 158).

Eine typische Frage der Schüler wird auf diesen ganzen Formelapparat sein:

``MUSS ICH DIE ALLE KÖNNEN?''

FAZIT:

Es ist viel wichtiger, den Schülern das Grundverständnis der Trigonometrie zu vermitteln, daß sie die Grundbeziehungen sin, cos und tan am allgemeinen und rechtwinkligen Dreieck und am Einheitskreis verstehen und anwenden können. Sie sollten auf keinen Fall mit einem solch riesigen Formelapparat erschlagen werden.