Didaktik Seminar
|
Hauptsatz
der elementaren Zahlentheorie
|
Mathematik
Didaktik Seminar |
Hauptsatz der elementaren Zahlentheorie
Die Produktdarstellung natürlicher Zahlen
Wir erinnern uns an den Darstellungssatz und die Definition eines Teilers t einer Zahl a:
t|a Þa=k·t
mit k![]() N
N
Beachtet man die Kommutativität
der Multiplikation, gilt auch a=t·k. Somit liefert der Darstellungssatz
bereits einen zweiten Teiler k, den zu t komplementären Teiler von a.
t hat als natürliche Zahl wieder Teiler. Angenommen j|t, dann gilt t=l·j
mit l![]() N.
N.
Insgesamt gilt für a:
a = k·l·j
Dieses Verfahren zur "Verfeinerung"
läßt sich bis zum Finden eines Teilers der eine Primzahl ist, eines
sog. Primteilers fortsetzen. Zerlegt man ebenfalls den Komplementärteiler,
so erhält man die Produktdarstellung der Zahl a. Diese besteht gänzlich
aus Primteilern, denn jeder Faktor der keine Primzahl ist, wäre noch weiter
zerlegbar.
Primzahlen haben somit als Produktdarstellung sich selbst. Alle anderen Zahlen
(bis auf 1) sind zusammengesetzt.
Beispiele:
|
a=180
|
|||
|
10
|
·
|
18
|
|
|
5·2
|
·
|
3·
|
6
|
|
5·2
|
·
|
3·
|
2·3
|
a=5·2·3·2·3=2·2·3·3·5=180
|
b=35256
|
|||||
|
8·
|
4407
|
||||
|
4·
|
2·
|
39·
|
113
|
||
|
2·
|
2·
|
2·
|
3·
|
13·
|
113
|
b=2·2·2·3·13·113=35256
Es bietet sich folgendes Verfahren an, um eine (in der Schule meist leicht zerlegbare) Zahl a in seine Primfaktoren zu zerlegen:
Finde den kleinsten Teiler
von a (Also 2 oder 3 oder ...) und schreibe ihn auf.
Teile a durch diesen Teiler.
Suche von der neuen Zahl wieder den kleinsten Teiler und notiere ihn.
Teile die neue Zahl durch den Teiler usw. bis du beim Teilen 1 erhältst.
Die gefundenen Teiler sind die Faktoren der Produktdarstellung von a.
Dieses Applet und diese Javascript-Version arbeiten nach diesem Prinzip.
Beispiele:
|
a
=180
|
|
a
= 35256
|
||
|
|
|
|
|
|
|
180
|
2
|
|
35256
|
2
|
|
90
|
2
|
|
17628
|
2
|
|
45
|
3
|
|
8814
|
2
|
|
15
|
3
|
|
4407
|
3
|
|
5
|
5
|
|
1469
|
13
|
|
1
|
|
|
113
|
113
|
|
|
|
|
1
|
|
|
a
= 2·2·3·3·5
|
|
|
|
|
|
|
|
|
a
= 2·2·2·3·13·113
|
|
Hauptsatz der elementaren Zahlentheorie
Wir fassen nun gleiche Faktoren durch Exponentialschreibweise zusammen und formulieren aus den oben gewonnenen Erkenntnissen den Hauptsatz der elementaren Zahlentheorie:
Sei n eine natürliche Zahl. Dann lässt sich n — bis auf die Reihenfolge — eindeutig in der Form
n = ![]() ·
·![]() ·...·
·...·![]()
darstellen. Darin sind p1,
p2, p3, ..., pm die der Größe nach
geordneten Primzahlen und es gilt für alle i: an![]() 0.
0.
Beispiele:
| a = 189 = 33·71 |
| a = 540 = 22·32·5 |
| a = 123456 = 26·3·643 |
| a = 99990001 = 999900011 |
Grafisch sieht eine mögliche Vorstellung der Zahl 540 damit so aus:
|
a
- Primfaktorpotenz
|
||||
|
3
|
||||
|
2
|
22
|
32
|
||
|
1
|
|
|
51
|
|
|
0
|
|
|
|
70
|
|
Primfaktor
|
2
|
3
|
5
|
7
|
Hat man mit Hilfe des Hauptsatzes
die Produktdarstellung zweier Zahlen a und b gewonnen, so kann man aus diesen
den ggT und das kgV direkt ablesen.
Den größten gemeinsamen Teiler erhält man, in dem man
alle gemeinsamen Faktoren von a und b zusammen fasst.
Beispiele:
| a =
220 = 2·2·5·11 b = 726 = 2·3·11·11 |
Þ ggT(220, 726) = 2·11 = 22 |
| a =
12348 = 2·2·3·3·7·7·7 b= 4444 = 2·2·11·101 |
Þ ggT(12348, 4444) = 2·2 = 4 |
Um das kleinste gemeinsame Vielfache zu erhalten, müssen alle in beiden Zahlen auftretenden Faktoren in der jeweils höchsten Potenz genommen werden.
Beispiele:
| a = 12 = 2·2·3 b = 18 = 2·3·3 |
Þ kgV(12, 18) = 2·2·3·3 = 36 |
| a = 40 = 2·2·2·5 b = 36 = 2·2·3·3 |
Þ kgV(40, 36) = 2·2·2·3·3·5 = 360 |
Übungen:
Fritzchen trippelt neben seinem großen Bruder einher. Seine Schrittlänge ist 30 cm, die seines Bruders 80cm. Nach wieviel Schritten setzen sie gleichzeitig a) einen Fuß, b den gleichen Fuß auf?
Zwei rechteckige Blechstücke (315cm lang, 75cm breit und 297cm lang, 90cm breit) sollen ohne Abfall in möglichst große gleichlange Rechtecke von 15cm Breite zerschnitten werden. Gib Länge und Anzahl der Stücke an!
Anzahl der Teiler und Teilersumme
Aus der Produktdarstellung laßt sich auch systematisch die Anzahl der Teiler und die Teilersumme berechnen. Ist z.B. die Zahl 360 = 23·32·5 gegeben, ergeben sich die Teiler 20·30·50, 20·30·51,20·31·50, 20·31·51, 20·32·50, usw (die Teiler sind dann allerdings nicht nach Größe geordnet). Im Endeffekt muss man alle möglichen Exponentenkombinationen aufspüren. Im Beispiel ergeben sich 4·3·2 = 24 mögliche Teiler - einschließlich 1 und 360.
Bezeichnet man die Anzahl der Teiler einer Zahl n mit t(n) ergeben sich im allgemeinen Fall mit
n = ![]() ·
·![]() ·...·
·...·![]()
t(n) = (a1+1)·(a2+1)·...·(am+1) mögliche Teiler.
Ebenso berechnet sich die mit s(n) bezeichnete Teilersumme. Für primes p ergibt sich für s(pn) (durch Anwendung der geometrischen Reihe):
|
s(pn) = 1 + p + p2 + p3 + ...+ pn = |
pn+1
- 1
———— p-1 |
Für zwei verschiedene Primfaktoren p und q ist
|
s(pn·qm) = |
pn+1
- 1
———— p-1 |
·
|
qm+1
- 1
———— q-1 |
| und damit für allgemeines |
n = |
|
|
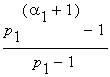 |
· |
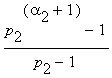 |
·...· |
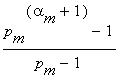 |