Unendlichkeitsbeweis

Mathematik Didaktik Seminar

Unendlichkeitsbeweis

Schon die Araber beschäftigten sich in der Zahlentheorie mit Primzahlen. Aber erst die alten Griechen legten ihre Erkenntnisse auch didaktisch aufbereitet nieder. Als das Paradebeispiel einer derartigen didaktischen Sammlung mathematischen Wissens gilt auch heute noch Euklids Werk "Die Elemente des Euklid" das ca. 325 v. Chr. entstand. Euklides von Alexandria wird auch die klassische Form des Unendlichkeitsbeweises zugeschrieben, obwohl diese sicherlich schon vor ihm bekannt war.

Euklid stellt im 9. Buch §20 die Behauptung auf "Es gibt mehr Primzahlen als jede vorgelegte Anzahl von Primzahlen".

Beweis:

"Die vorgelegten Primzahlen seien a,b,c. Ich behaupte, dass es mehr Primzahlen gibt als a,b,c.
Man bilde die kleinste von a,b,c gemessene [geteilte] Zahl; sie sei DE und man füge zu DE die Einheit DF hinzu.

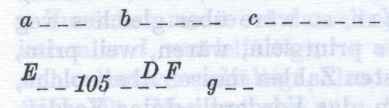
Entweder ist EF dann eine Primzahl oder nicht. Zunächst sei es eine Primzahl. Dann hat man mehr Primzahlen als a,b,c, nämlich a,b,c, EF.
Zweitens sei EF keine Primzahl. Dann muß es aber von irgendeiner Primzahl gemessen [geteilt] werden; es werde von der Primzahl g gemessen [geteilt]. Ich behaupte, daß g mit keiner der Zahlen a,b,c zusammenfällt. Wenn möglich tue es dies nämlich. a,b,c messen [geteile] nun DE; auch g müßte dann DE messen [teilen]. Es misst [teilt] aber auch EF. g müßte also auch den Rest, die Einheit DF messen [teilen], während es eine Zahl ist; dies wäre Unsinn. Also fällt g mit keiner der Zahlen a,b,c zusammen; und es ist Primzahl nach Voraussetzung. Man hat also mehr Primzahlen als die vorgelegte Anzahl a,b,c gefunden, nämlich a,b,c,g - q.e.d."
(Erläuterung: eine Einheit ist ein Element mit Inversen (in N nur 1)).

In "moderner" mathematischer Sprache

Angenommen es gibt genau n Primzahlen.
Seien diese n Primzahlen mit p₁, p₂, p₃, ..., p_n gegeben.

Sei x = p₁·p₂·p₃·...·p_n + 1.

x ist durch kein p_i teilbar, denn x hat immer der Rest 1 beim Teilen mit p_i.
x hat aber mindestens einen Primteiler > 1. Dieser Primteiler muss eine neue Primzahl sein
Þ Zu jeder vorgegebenen Anzahl n von Primzahlen lässt sich immer eine weitere finden
Þ Es gibt unendlich viele Primzahlen