Primzahlverteilung

Mathematik Didaktik Seminar

Primzahlverteilung

Wie anfangs erwähnt, gibt es keine Konstruktionsvorschrift für Primzahlen , weil "... die Primzahlen, trotz ihrer einfachen Definition und Rolle als Bausteine der natürlichen Zahlen, zu den willkürlichsten, widerspenstigsten Objekten gehören, die der Mathematiker überhaupt studiert. Sie wachsen wie Unkraut unter den natürlichen Zahlen, scheinbar keinem anderen Gesetz als dem Zufall unterworfen, und kein Mensch kann voraussagen, wo wieder eine sprießen wird, noch einer Zahl ansehen, ob sie prim ist oder nicht." (Don Zagier)

Gleichzeitig gehorchen die Primzahlen aber auch gewissen Gesetzmäßigkeiten. Insbesondere deren Verteilung unter den natürlichen Zahlen lässt sich statistisch erstaunlich gut beschreiben. Wieder war es Gauß, der als Fünfzehnjähriger einen Zusammenhang fand und im Primzahlsatz formulierte.

Mit p(x) bezeichnete er die Anzahl der Primzahlen bis x.

Für p(x) ergiebt sich für 0x100 folgender Graph:

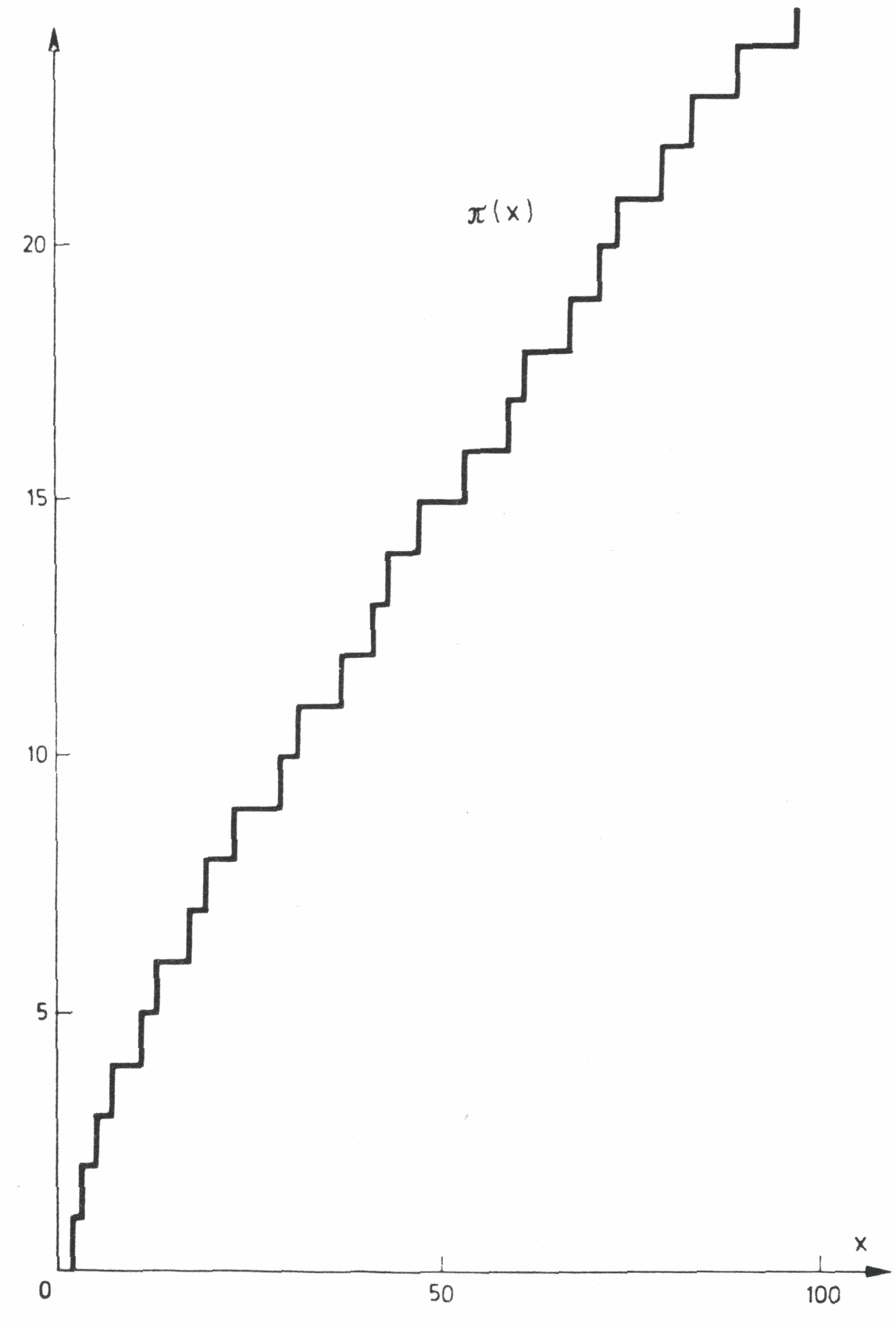
Dehnt man das Betrachtungsintervall aus, erhält man diese erstaunliche Veranschaulichung:

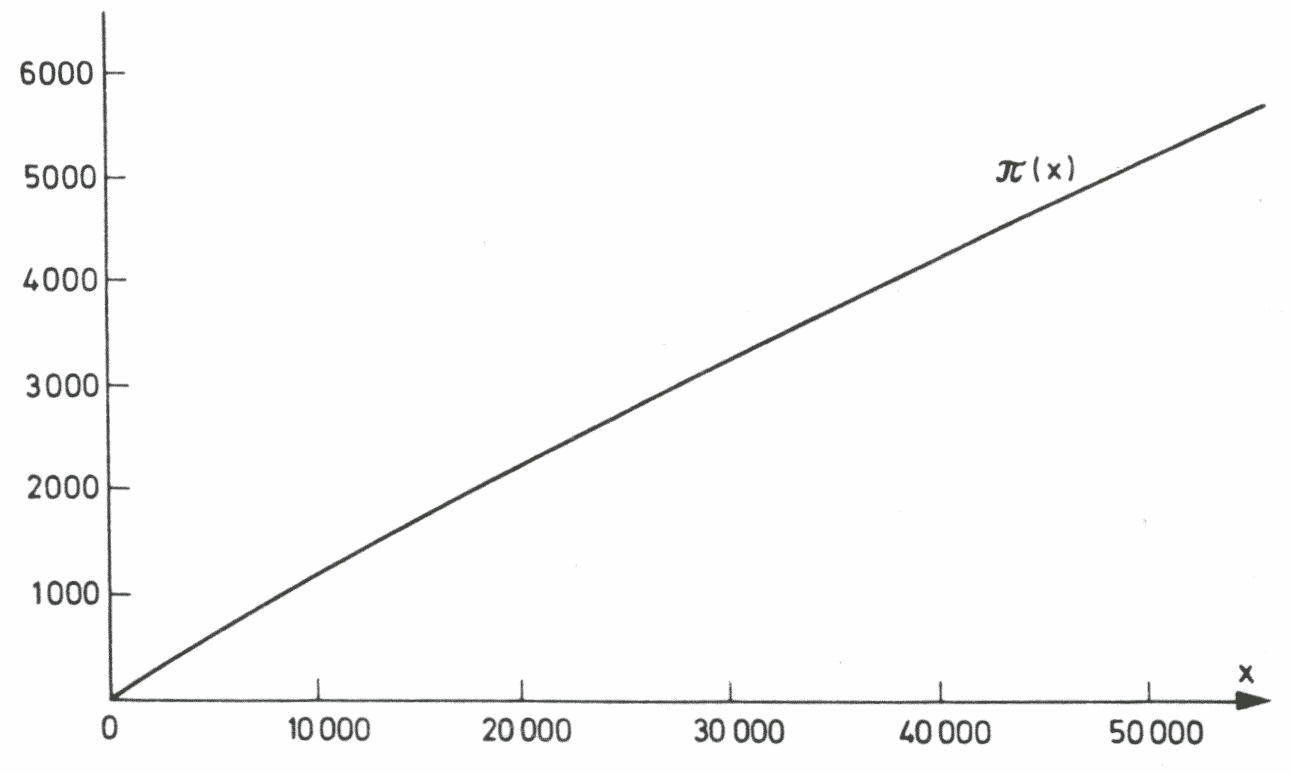
In Zahlen sieht das ganze folgendermaßen aus:

Gauß hatte anhand ähnlicher Daten den Verdacht, dass das Verhältnis von x zu p(x) immer um den Faktor 2,3 ansteigt, wenn die Zehnerpotenz zur nächsten übergeht. Da 2,3 = ln(10) stellte er folgende Vermutung auf:

p(x) ~

Mit umfangreicheren Daten über p(x) stellte Legendre 1808 eine noch bessere Näherung auf:

p(x) ~

Ein anderer Ansatz, ebenfalls von Gauß, geht von der empirischen Tatsache aus, dass die Frequenz der Primzahlen um eine sehr grosse Zahl fast genau gleich 1 / ln(x) ist. Dadurch lassen sich erstaunlich präzise Vorhersagen über Primzahlen machen.
Demnach wäre die Anzahl der Primzahlen in einen Intervall der Länge a ungefähr a / lnx, wenn a klein genug im Vergleich zu x ist. Entsprechend ist die Wahrscheinlichkeit, dass zwei vorgegebene Zahlen in der Nähe von x beide prim sind 1 / ln²x. Möchte man nun wissen, wieviel Primzahlzwillinge es in einem Intervall von x bis x+a gibt, so erwartet man ungefähr a/ ln²x. In der Tat sind es etwas mehr, denn ist ein primes n gefunden, so ist n+2 ungerade und damit wahrscheinlicher prim. Heuristische Argumente liefern eine Konstante von ungefähr 1,32·a/ ln²x.

Die Übereinstimmung mit der Theorie ist recht gut, wie folgende Tabelle belegt: