Didaktik Seminar
|
Primzahlen
|
Mathematik
Didaktik Seminar |
Einführung
Betrachtet man die Teilermengen
einiger spezieller Zahlen, so fällt auf, dass diese nur aus der 1 und der
Zahl selbst bestehen. Solche Zahlen die nur durch 1 und sich selbst teilbar
sind bezeichnet man als Primzahlen (lat.: primordinal = von erster Ordnung,
uranfänglich, ursprünglich).
Die Reihe der Primzahlen beginnt mit 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,
....
Die Primzahl-Eigenschaft ist seit dem Beginn zahlentheorethischer Überlegungen bekannt. Aufgrund ihrer schwer durchschaubaren Gesetze ist sie auch heute noch von besonderem Interesse. So ist zwar bewiesen, dass unendlich viele ihrer Art existieren, eine Gesetzmäßigkeit für die Verteilung von Primzahlen in den natürlichen Zahlen gibt es jedoch nicht. So hat sich, im Laufe der Jahrhunderte, eine regelrechte Jagd auf große und vor allem die größte Primzahl entwickelt. Diese wird durch die Möglichkeit der Computerunterstützung noch beschleunigt. Als besonders ergiebig hat sich die Suche unter den sogenannten Mersennschen Zahlen der Form Mn=2n-1 herausgestellt.
Anhand der folgenden Tabelle (siehe Primepages) lassen sich die Anstrengungen der Mathematiker nachvollziehen, die noch nicht über Computer verfügten:
| Zahl | Stellen | Jahr | Mathematiker | Methode |
|---|---|---|---|---|
| 217-1 | 6 | 1588 | Cataldi | Versuchsweise |
| 219-1 | 6 | 1588 | Cataldi | Versuchsweise |
| 231-1 | 10 | 1772 | Euler | Versuchsweise |
| (259-1)/179951 | 13 | 1867 | Landry | Versuchsweise |
| 2127-1 | 39 | 1876 | Lucas | Lucas sequences |
| (2148+1)/17 | 44 | 1951 | Ferrier | Proth's theorem |
Dank verbesserter Testverfahren und der schneller werdenden Computer wurden die gefundenen Primzahlen schnell größer:
| Zahl | Stellen | Jahr | Rechner | Mathematiker(-Team) |
|---|---|---|---|---|
| 180(M127)2+1 | 79 | 1951 | EDSAC1 | Miller & Wheeler |
| M521 | 157 | 1952 | SWAC | Robinson (Jan 30) |
| M607 | 183 | 1952 | SWAC | Robinson (Jan 30) |
| M1279 | 386 | 1952 | SWAC | Robinson (June 25) |
| M2203 | 664 | 1952 | SWAC | Robinson (Oct 7) |
| M2281 | 687 | 1952 | SWAC | Robinson (Oct 9) |
| M3217 | 969 | 1957 | BESK | Riesel |
| M4423 | 1332 | 1961 | IBM7090 | Hurwitz |
| M9689 | 2917 | 1963 | ILLIAC 2 | Gillies |
| M9941 | 2993 | 1963 | ILLIAC 2 | Gillies |
| M11213 | 3376 | 1963 | ILLIAC 2 | Gillies |
| M19937 | 6002 | 1971 | IBM360/91 | Tuckerman |
| M21701 | 6533 | 1978 | Cyber 174 | Noll & Nickel |
| M23209 | 6987 | 1979 | Cyber 174 | Noll |
| M44497 | 13395 | 1979 | Cray 1 | Nelson & Slowinski |
| M86243 | 25962 | 1982 | Cray 1 | Slowinski |
| M132049 | 39751 | 1983 | Cray X-MP | Slowinski |
| M216091 | 65050 | 1985 | Cray X-MP | Slowinski |
| 391581*2216193-1 | 65087 | 1989 | Amdahl 1200 | Amdahl Six |
| M756839 | 227832 | 1992 | Cray-2 | Slowinski & Gage |
| M859433 | 258716 | 1994 | Cray C90 | Slowinski & Gage |
| M1257787 | 378632 | 1996 | Cray T94 | Slowinski & Gage |
| M1398269 | 420921 | 1996 | Pentium (90 Mhz) | Armengaud, Woltman, et. al. [GIMPS] |
| M2976221 | 895932 | 1997 | Pentium (100 Mhz) | Spence, Woltman, et. al. [GIMPS] |
| M3021377 | 909526 | 1998 | Pentium (200 Mhz) | Clarkson, Woltman, Kurowski, et. al. [GIMPS, PrimeNet] |
| M6972593 | 2098960 | 1999 | Pentium (350 Mhz) | Hajratwala, Woltman, Kurowski, et. al. [GIMPS, PrimeNet] |
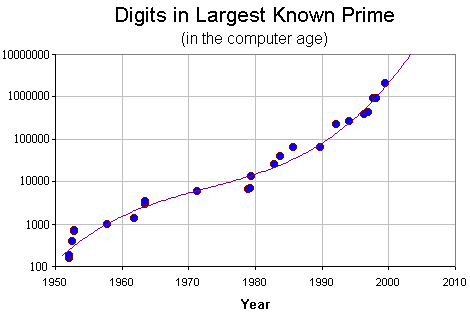
Folgende Grafik verdeutlicht wie schnell die gefundenen Primzahlen immer größer werden: