Teiler
und Vielfache
 |
 |
 |
Mathematik
Didaktik Seminar
Didaktik Seminar
|
Teiler
und Vielfache
|
|
Mathematik
Didaktik Seminar |
Teiler und Vielfache
Ergeben sich für zwei
natürliche Zahlen a, b aus dem Darstellungssatz die zugehörigen Zahlen
k, r und gilt r=0,
so heißt b Teiler von a, geschrieben b|a. Außerdem heißt
a Vielfaches von b.
Damit ist a=0 Vielfaches für alle natürlichen Zahlen.
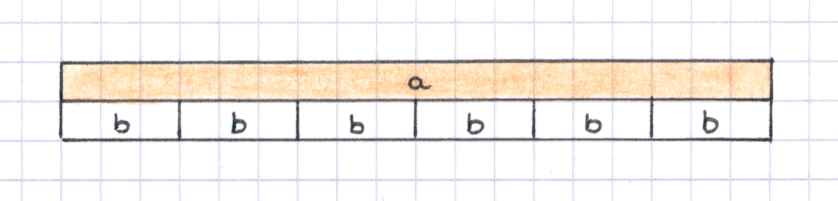
Beispiele:
| a=24; b=6 | 24 = 4 · 6 + 0 |
also ist 6 Teiler von 24 und 24 Vielfaches von 6 |
| a=38399051, b=163 | 38399051=235577 · 163 + 0 | also ist 163 Teiler von a und a ein Vielfaches von 163 |
| a=20; b=7 | 20=2 · 7 + 6 | also ist 7 kein Teiler von a und a kein Vielfaches von 7 |
Teilermenge und Vielfachenmenge
|
Schneide einen Streifen Papier mit einer Länge von 24 Kästchen. Wieviele Möglichkeiten gibt es, diesen Streifen ein- oder mehrmals zu falten, ohne dass etwas übersteht bzw. beim letzten Falten der Streifen zu kurz ist? In welchen Bezug stehen die (gültigen) Möglichkeiten zur Zahl 24? Offensichtlich erhält man mit dieser Forderung alle Teiler der Zahl 24. |
Fasst man alle Teiler b
einer natürlichen Zahl a zu einer Menge zusammen, so erhält man die
Teilermenge von a.
Die Teilermenge einer Zahl a wird mit Ta
bezeichnet.
Ta
enthält stets die Teiler 1 und a, die deshalb auch als uneigentliche
Teiler bezeichnet werden.
Da außerdem immer gilt, dass a
k·b
ist die Teilermenge endlich.
Beispiel:
| a=20 | T20={1, 2, 4, 5, 10, 20} |
| a=60 | T60={1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60} |
| a=1112222 | T1112222={1, 2, 19, 38, 29269, 58538, 556111, 1112222} |
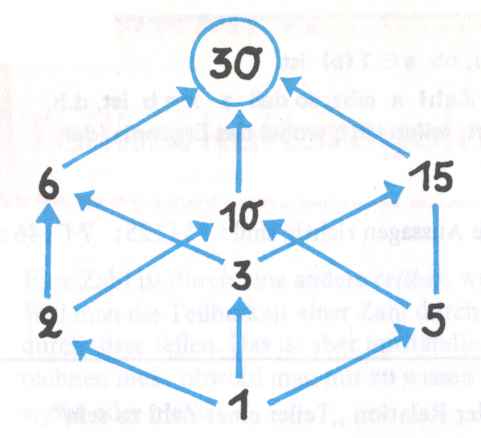
Anschaulich lässt sich die Teilermenge mit sogenannten Teilergrafen darstellen, z.B. für die Zahl 30:
Fasst man hingegen alle Vielfachen einer Zahl a zusammen, so erhält man
die Vielfachenmenge Va.
Da 0 ein Vielfaches jeder Zahl ist, ist 0 immer Bestandteil einer Vielfachenmenge.
Beispiel:
| a=3 | V3={0, 3, 6, 9, 12, 15, ...} |
| a=15 | V15={0, 15, 30, 45, 60, 75, 80, ...} |
| a=166 | V166={0, 166, 332, 498, 664, 830, 996, 1162, ...} |
Übungen:
Bestimme die Teilermengen von 29, 30, 128, 129, 499 und zeichne ihre Teilergrafen!