Didaktik Seminar
|
Gemeinsame
Teiler und Vielfache
|
Mathematik
Didaktik Seminar |
Gemeinsame Teiler und der ggT
Die geometrische Vorstellung der "Ganzzahligen Streifen" lässt noch weitere Fragen zu. Eine davon ist die Frage, ob es einen Streifen t gibt mit dem sich zwei verschieden lange Streifen a und b jeweils ganzzahlig auslegen lassen. Dazu müsste gelten:
t|a : 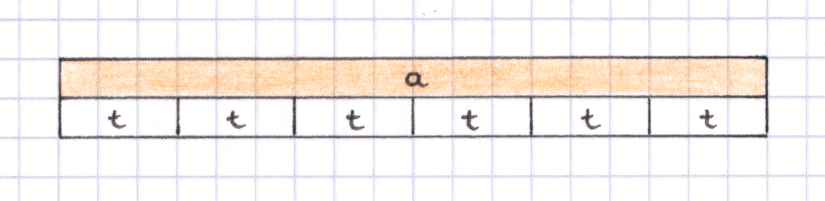
und
t|b : 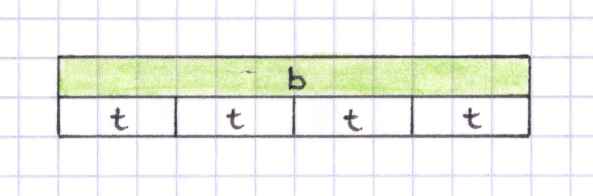
t muss also ein gemeinsamer
Teiler von a und von b sein. Man findet solche t in dem man die beiden Teilermengen
Ta und Tb schneidet.
In der entstehenden Schnittmenge S gibt es immer ein größtes Element,
den größten gemeinsamen Teiler von a und b, kurz ggT(a,b).
Alle Teiler des ggT(a,b) sind immer auch Teiler von a und von b.
Ist der größte gemeinsame Teiler zweier Zahlen 1, so sind die Zahlen teilerfremd, weil sie nur den uneigentlichen Teiler 1 besitzen.
Beispiele:
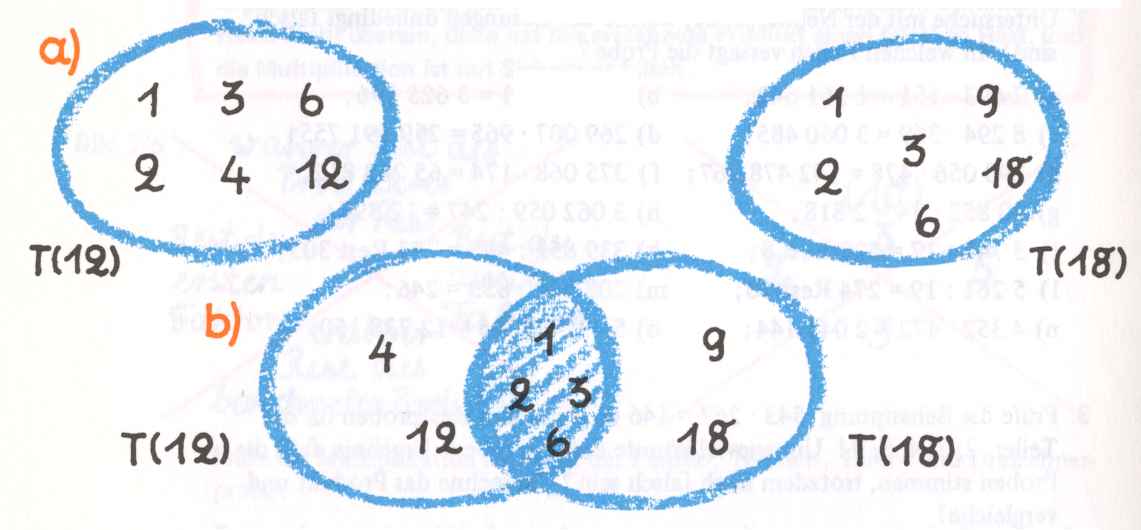
|
a=12 Þ T(12)={1,2,3,4,6,12} b=18 Þ T(18)={1,2,3,6,9,18} |
Also
sind 1, 2, 3, 6 gemeinsame Teiler von a und b. 6 ist der größte gemeinsame Teiler von 12 und 18. |
|
a=48 Þ T(48)={1,2,3,4,6,8,12,16,24,48} b=56 Þ
|
Als Schnittmenge ergiebt sich S={1, 2, 4, 8}. Damit ist 8 der ggT von 48 und 56. |
Gemeinsame Vielfache und das kgV
Welche Zahlen sind sowohl Vielfache von a und von b? Um sie zu finden bildet man Va und Vb. Alle Zahlen die sowohl Vielfaches von a als auch von b sind, sind den Vielfachenmengen Va und Vb gemeinsam. Solche Elemente findet man durch Mengendurchschnittsbildung S = Va Ç Vb.
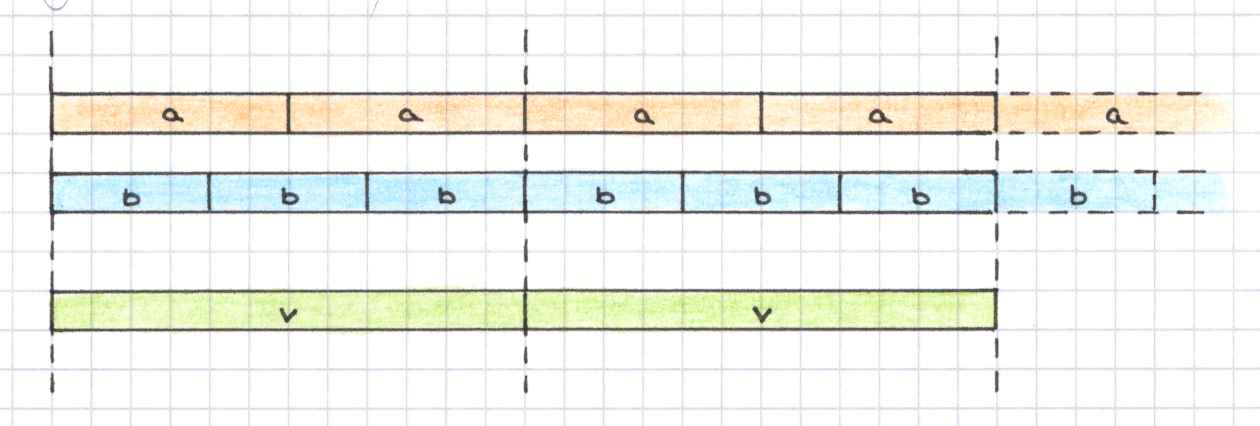
Geometrisch bedeutet dies, a immer wieder aneinander zu legen, b immer wieder aneinander zu legen und nach Streifen v zu suchen, die ein Vielfaches von a und von b sind.
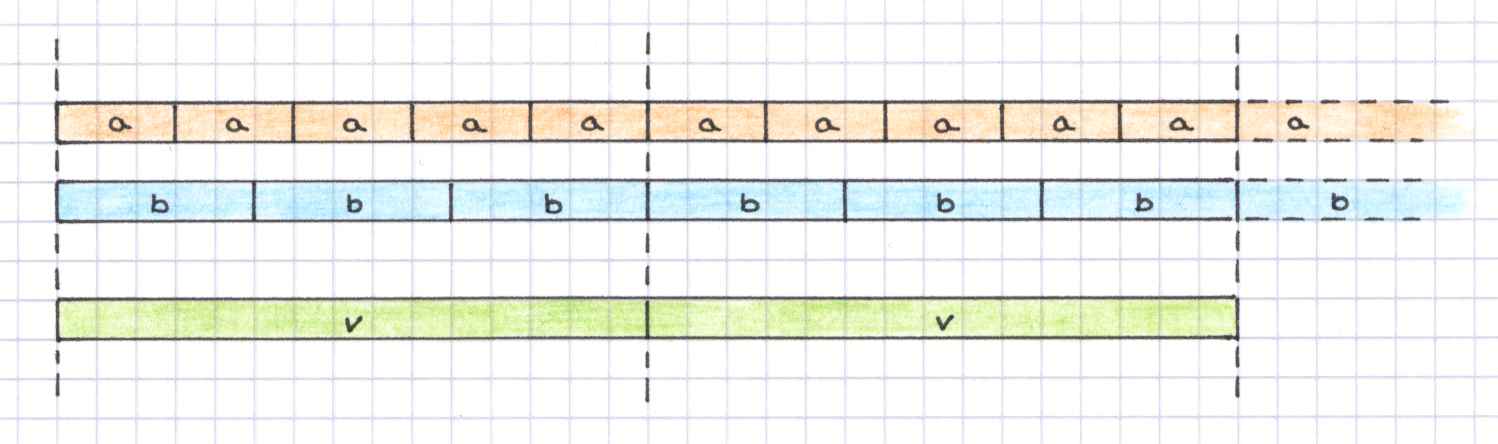
Die gemeinsamen Elemente
von Va
und Vb
heißen gemeinsame Vielfache von a und b.
Anschaulich sieht man sofort, dass a und b immer gemeinsame Vielfache haben,
denn mindestens ein gemeinsames Vielfaches findet man, indem man a mal b aneinander
legt.
Es gibt dann auch ein kleinstes gemeinsames Vielfaches, kurz kgV, in S. Sind a und b teilerfremd, ist dies genau a·b.
| Andernfalls gilt: kgV(a,b) = |
a·b
———— ggT(a,b) |
Hier im Beispiel:
a=3 Þ V3={0,3,6,9,12,15,18,21,24,27,30,33,...}
b=5 Þ V5={0,5,10,15,20,25,30,35,...}
Gemeinsame Vielfache sind also V6 Ç V4={0, 15, 30, ...}
Bei einem anderen Beispiel mit den Zahlen a=6, b=4 findet man:
V6={0,6,12,18,24,30,36,...}
V4={0,4,8,12,16,20,24,28,32,36,...}
Gemeinsame Vielfache sind somit V6 Ç V4={0, 12, 24, 36, ...}
| Der ggT(6,4)=2 Þ kgV(6,4)= |
6·4
———— 2 |
=12
|
Übungen:
| Zwei
Zahnräder mit 30 bzw. 25 Zähnen greifen ineinander und drehen
sich. Nach wieviel Umdrehungen liegen die Punkte wieder so zueinander wie
in der Abbildung? |
 |
Die Klassenkameraden Martin, Heike und Elke gehen seit dem ersten Ferientag regelmäßig zum Schwimmen. Martin geht jeden drittenTag, Heike jeden vierten Tag und Elke jeden sechsten Tag. An welchen Tagen sind zwei (drei) von ihnen im Schwimmbad?